Maximizing the retention level for proportional reinsurance under -regulation of the finite time surplus process with unit-equalized interarrival time
Keywords:
Probability of insolvency, Proportional reinsurance, Maximal retention levelAbstract
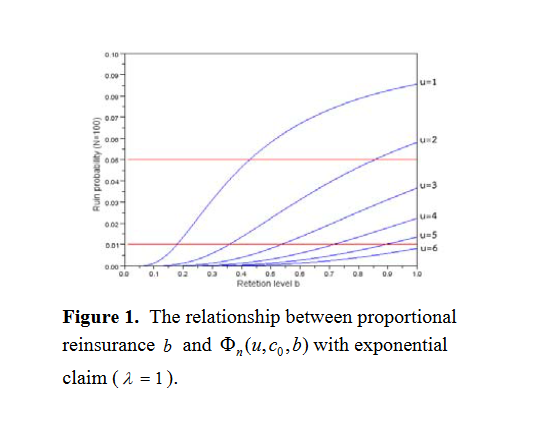
The research focuses on an insurance model controlled by proportional reinsurance in the finite-time surplus process with a unit-equalized time interval. We prove the existence of the maximal retention level for independent and identically distributed claim processes under α-regulation, i.e., a model where the insurance company has to manage the probability of insolvency to be at most α. In addition, we illustrate the maximal retention level for exponential claims by applying the bisection technique.
References
Chan, W. S., & Zhang, L. (2006). Direct derivation of finite-time ruin probabilities in the discrete risk model with exponential or geometric
claims. North American Actuarial Journal, 10 (4), 269-279.
Klongdee, W. (2013). On the existence of maximal retention level for proportional reinsurance under -regulation. Far East Journal of
Mathematical Sciences (FJMS), Special (2013),333-338.
Sattayatham, P., et.al. (2013). Ruin Probability-Base Initial Capital of the Discrete-Time Surplus Process. Variance. 7(1), 74-81.
Schal, M. (2004). On discrete-time dynamic programming in insurance: exponential utility & maximizing the ruin probability. Scand.
Actuarial Journal, 3, 189-210.
Supawan, K. (2015). A sufficient condition for reducing the finite-time probability of insolvency under proportional reinsurance in
discrete-time surplus process. Far East Journal of Mathematical Sciences (FJMS). 96(5), 641-650.