Numerical Approximations of Fredholm-Volterra Integral Equation of 2nd kind using Galerkin and Collocation Methods
Keywords:
Fredholm-Volterra integral equations, Galerkin method, collocation method, polynomialsAbstract
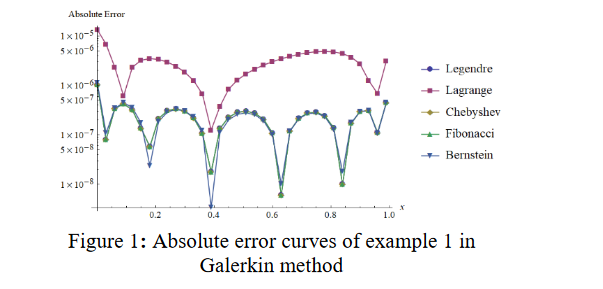
Galerkin and collocation approximation techniques are very effective and popular among researchers for numerical approximations of different types of differential, integral and integro-differential equations. Both methods approximate the solution by a finite sum of some known polynomials. In recent years, researchers around the world have been used different combinations of polynomials and collocation points in Galerkin and collocation methods for numerical approximations of different types of integral equations. Also, collocation method have been used more frequently compared to the Galerkin method. In this research, five different polynomials in
Galerkin method and five different combinations of polynomials and collocation points in collocation method have been used for numerical approximations of linear FVIE of 2nd kind.It is found that the performances of different polynomials and collocation points in both these methods are consistent.
References
Dastjerdi, H. L. & Ghaini, F. M. M. ( 2012) .Numerical solution of Volterra- Fredholm integral equations by moving least square
method and Chebyshev polynomials. Applied Mathematics Modelling, 36, 3283-3288.doi:10.1016/j.apm.2011.10.005
Ebrahimi, N. & Rashidinia, J. ( 2015). Collocation method for linear and nonlinear Fredholm and Volterra integral equations. Applied
Mathematics and Computation, 270, 156-164.doi: 10.1016/j.amc.2015.08.032
Hesameddini, E. & Shahbazi, M. ( 2017) . Solving system of Volterra- Fredholm integral equations with Bernstein polynomials and
hybrid Bernstein block- pulse functions.Journal of Computational and Applied Mathematics, 315, 182- 194. doi:10.1016/j.cam.2016.11.004
Liu, H. , Huang, J. , Pan, Y. & Zhang, J. ( 2018) . Barycentric interpolation collocation methods for solving linear and nonlinear high-
dimensional Fredholm integral equations.Journal of Computational and Applied Mathematics, 327, 141- 154. doi:10.1016/j.cam.2017.06.004
Mandal, B. N. & Bhattacharya, S. (2007). Numerical solution of some classes of integral equations using Bernstein polynomials. Applied
Mathematics and Computation, 190, 1707-1716.doi: 10.1016/j.amc.2007.02.058
Mirzaee, F. & Hoseini, S. F. (2016). Application of Fibonacci collocation method for solving Volterra-Fredholm integral equations. Applied
Mathematics and Computation, 273, 637-644.doi: 10.1016/j.amc.2015.10.035
Molla, H. U. & Saha, G. ( 2018) . Numerical approximation of Fredholm integral equation( FIE) of 2nd kind using FE- Galerkin and
collocation methods. GANIT: Journal of Bangladesh Mathematical Society, 38,11-25.doi:10.3329/ganit.v38i0.39782
Nemati, S. (2015). Numerical solution of Volterra-Fredholm integral equations using Legendre collocation method. Journal of Computational
and Applied Mathematics, 278, 29- 36. doi:10.1016/j.cam.2014.09.030
Wang, K. & Wang, Q. (2013). Lagrange collocation method for solving Volterra-Fredholm integral equations. Applied Mathematics and
Computation, 219, 10434- 10440. doi:10.1016/j.amc.2013.04.017
Wang, K. & Wang, Q. ( 2014) . Taylor collocation method and convergence analysis for the Volterra-Fredholm integral equations. Journal
of Computational and Applied Mathematics, 260, 294-300.doi: 10.1016/j.cam.2013.09.050
Yousuf, S. & Razzaghi, M. ( 2005) . Legendre wavelets method for the nonlinear Volterra-Fredholm integral equations. Mathematics and
Computers in Simulation, 70, 1- 8. doi:10.1016/j.matcom.2005.02.035