A New Type of Extended Soft Set Operation: Complementary Extended Union Operation
DOI:
https://doi.org/10.53848/ssstj.v11i2.837Keywords:
Soft set, Complementary extended soft set operations, Hemiring, AlgebrasAbstract
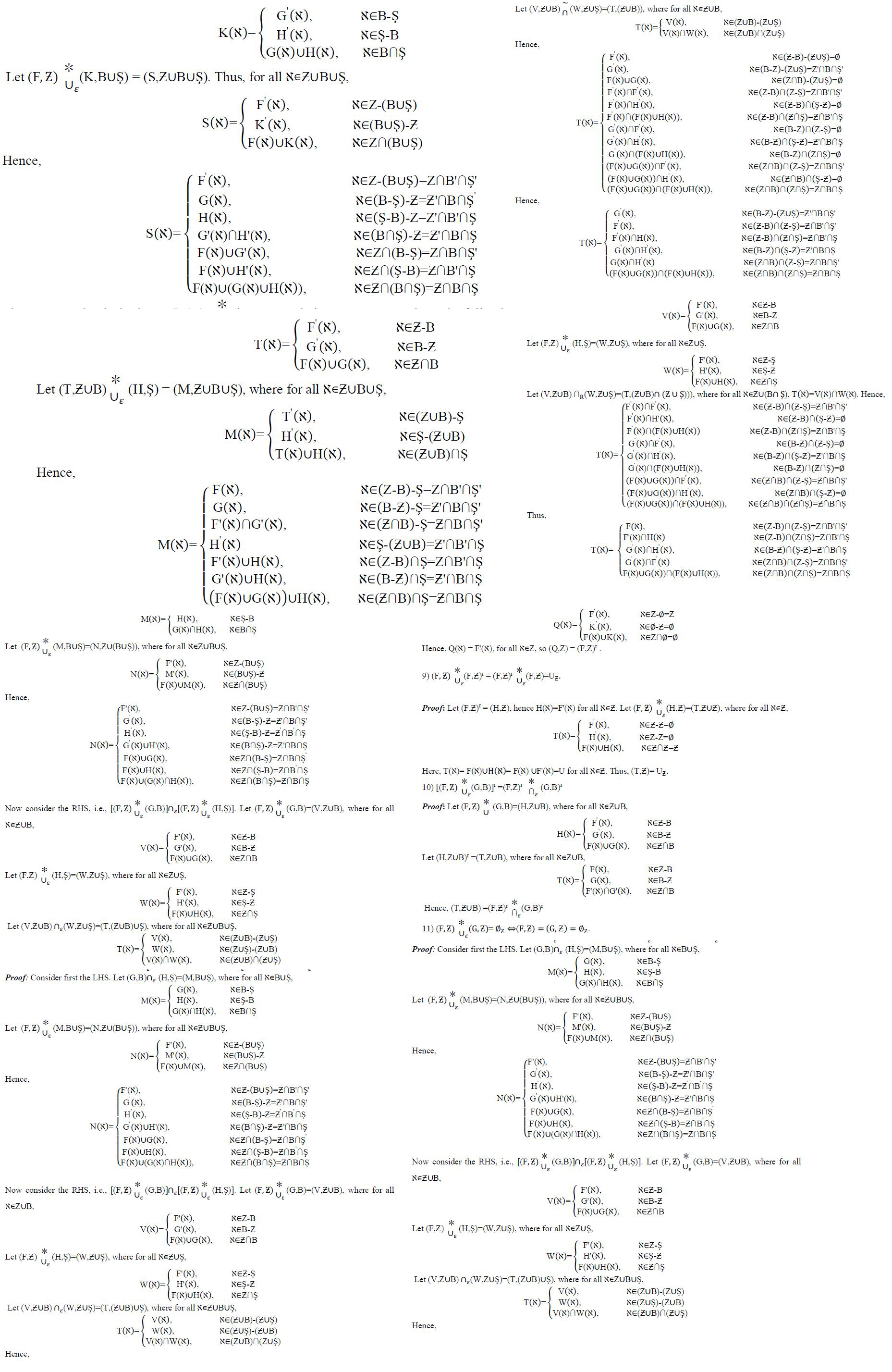
Soft set theory was proposed by Molodtsov in 1999 to model some problems involving uncertainty. It has a wide range of theoretical and practical applications. Soft set operations constitute the basic building blocks of soft set theory. Many kinds of soft set operations have been described and applied in various ways since the inception of the theory. In this paper, to contribute to the theory, a new soft set operation, called complementary extended union operation, is defined, its properties are discussed in detail to obtain the relationship of each operation with other soft set operations, and the distributions of these operations over other soft set operations are examined. We obtain that the complementary extended union operation along with other certain types of soft set operations construct some well-known algebraic structure such as Boolean Algebra, De Morgan Algebra, semiring, and hemiring in the set of soft sets with a fixed parameter set. Since Boolean Algebra is fundamental in digital logic design, computer science, information retrieval, set theory and probability; De Morgan Algebra in logic and set theory, computer science, artificial intelligence, circuit design; semirings in theoretical computer science, optimization problems, economics, cryptography and coding theory, and hemirings in combinatorics, mathematical economics, theoretical computer science, these algebraic structures provide essential tools for various applications, facilitating the analysis, design, and optimization of systems across many disciplines, and thus this study is expected to contribute to decision-making methods and cryptography based on soft sets.
References
References
Abbas, M., Ali, B., & Romaguera, S. (2014). On generalized soft equality and soft lattice structure. Filomat, 28(6), 1191-1203.
Abbas, M., Ali, M. I., & Romaguera, S. (2017). Generalized operations in soft set theory via relaxed conditions on parameters. Filomat, 31(19), 5955-5964.
Akbulut, E. (2024). New type of extended operations of soft sets: Complementary extended lambda and difference operation (Master’s thesis). Amasya University, Graduate School of Natural and Applied Sciences, Amasya, Türkiye.
Ali, M. I., Feng, F., Liu, X., Min, W. K., & Shabir, M. (2009). On some new operations in soft set theory. Computers and Mathematics with Applications, 57(9), 1547-1553.
Ali, M. I., Mahmood, T., Rehman, M. M., & Aslam, M. F. (2015). On lattice ordered soft sets. Applied Soft Computing, 36, 499-505.
Ali, M. I., Shabir, M., & Naz, M. (2011). Algebraic structures of soft sets associated with new operations. Computers and Mathematics with Applications, 61(9), 2647-2654.
Al-shami, T. M. (2019). Investigation and corrigendum to some results related to g-soft equality and gf-soft equality relations. Filomat, 33(11), 3375-3383.
Al-shami, T. M., & El-Shafei, M. E. (2020). T-soft equality relation. Turkish Journal of Mathematics, 44(4), 1427-1441.
Atagün, A. O., & Sezgin, A. (2018). Soft subnear-rings, soft ideals and soft N-subgroups of near-rings. Mathematical Sciences Letters, 7(1), 37-42.
Aybek, F. (2024). New restricted and extended soft set operations (Master’s thesis). Amasya University, Graduate School of Natural and Applied Sciences, Amasya, Türkiye.
Birkhoff, G. (1967). Lattice theory. Providence, Rhode: American Mathematical Society.
Çağman, N. (2021). Conditional complements of sets and their application to group theory. Journal of New Results in Science, 10(3), 67-74.
Çağman, N., Çıtak, F., & Aktaş, H. (2012). Soft int-group and its applications to group theory. Neural Computing and Applications, 21, 151-158.
Chang, C. C. (1959). A new proof of the completeness of the łukasiewicz axioms. Transactions of the American Mathematical Society, 93(1), 460-490.
Clifford, A. H. (1954). Bands of semigroups. Proceedings of the American Mathematical Society, 5(3), 499-504.
Demirci, A. M. (2024). New type of extended operations of soft sets: Complementary extended union, plus and theta operations Master’s thesis). Amasya University, Graduate School of Natural and Applied Sciences, Amasya, Türkiye.
Eren, Ö. F., & Çalışıcı, H. (2019). On some operations of soft sets. The Fourth International Conference on Computational Mathematics and Engineering Sciences (CMES 2019), Antalya.
Feng, F., Li, C., Davvaz, B., & Ali, M. I. (2010). Soft sets combined with fuzzy sets and rough sets: A tentative approach. Soft Computing, 14, 899-911.
Feng, F., & Li, Y. (2013). Soft subsets and soft product operations. Information Sciences, 232, 44-57.
Fu, L. (2011). Notes on soft set operations. ARPN Journal of Systems and Software, 1(6), 205-208.
Ge, X., & Yang, S. (2011). Investigations on some operations of soft sets. World Academy of Science, Engineering and Technology, International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 5(3), 370-373.
Husain, S., & Shivani, K. (2018). A study of properties of soft set and its applications. International Research Journal of Engineering and Technology, 5(1), 363-372.
Iftikhar, M., & Mahmood, T. (2018). Some results on lattice ordered double framed soft semirings. International Journal of Algebra and Statistics, 7(1-2), 123-140.
Jana, C., Pal, M., Karaaslan, F., & Sezgin, A. (2019). (α, β)-Soft intersectional rings and ideals with their applications. New Mathematics and Natural Computation, 15(2), 333-350.
Jiang, Y., Tang, Y., Chen, Q., Wang, J., & Tang, S. (2010). Extending soft sets with description logics. Computers and Mathematics with Applications, 59(6), 2087-2096.
Jun, Y. B., & Yang, X. (2011). A note on the paper “Combination of interval-valued fuzzy set and soft set” [Comput. Math. Appl. 58 (2009) 521-527]. Computers and Mathematics with Applications, 61(5), 1468-1470.
Liu, X., Feng, F., & Jun, Y. B. (2012). A note on generalized soft equal relations. Computers and Mathematics with Applications, 64(4), 572-578.
Mahmood, T. (2020). A novel approach toward bipolar soft sets and their applications. Journal of Mathematics, 2020, 1-11.
Mahmood, T., Rehman, Z. U., & Sezgin, A. (2018). Lattice ordered soft near rings. Korean Journal of Mathemtics, 26(3), 503-517.
Maji, P. K, Biswas, R., & Roy, A. R. (2003). Soft set theory. Computers and Mathematics with Applications, 45(4-5), 555-562.
Molodtsov, D. (1999). Soft set theory-First results. Computers and Mathematics with Applications, 37(4-5), 19-31.
Muştuoğlu, E., Sezgin, A., & Türk, Z. K. (2016). Some characterizations on soft uni-groups and normal soft uni- groups. International Journal of Computer Applications, 155(10), 1-8.
Neog, T. J., & Sut, D. K. (2011). A new approach to the theory of soft sets. International Journal of Computer Applications, 32(2), 1-6.
Onyeozili, I. A., & Gwary, T. M. (2014). A study of the fundamentals of soft set theory. International Journal of Scientific & Technology Research, 3(4), 132-143.
Özlü, Ş., & Sezgin, A. (2020). Soft covered ideals in semigroups. Acta Universitatis Sapientiae, Mathematica, 12(2), 317-346.
Pant, S., Dagtoros, K., Kholil, M. I., & Vivas, A. (2024). Matrices: Peculiar determinant property. Optimum Science Journal, 1, 1-7.
Park, J. H., Kim, O. H., & Kwun, Y. C. (2012). Some properties of equivalence soft set relations. Computers and Mathematics with Applications, 63(6), 1079-1088.
Pei, D., & Miao, D. (2005). From soft sets to information systems. IEEE International Conference on Granular Computing, 2, 617-621.
Sarıalioğlu, M. (2024). New type of extended operations of soft sets: Complementary extended intersection, gamma and star operations (Master’s thesis). Amasya University, Graduate School of Natural and Applied Sciences, Amasya, Türkiye.
Sen, J. (2014). On algebraic structure of soft sets. Annals of Fuzzy Mathematics and Informatics, 7(6), 1013-1020.
Sezer, A. S. (2014). Certain characterizations of LA-semigroups by soft sets. Journal of Intelligent and Fuzzy Systems, 27(2), 1035-1046.
Sezer, A. S., Çağman, N., & Atagün, A. O. (2015). Uni-soft substructures of groups. Annals of Fuzzy Mathematics and Informatics, 9(2), 235-246.
Sezgin, A. (2016). A new approach to semigroup theory I: Soft union semigroups, ideals and bi-ideals. Algebra Letters, 2016, 1-46.
Sezgin, A. (2018). A new view on AG-groupoid theory via soft sets for uncertainty modeling. Filomat, 32(8), 2995-3030.
Sezgin, A., Ahmad, S., & Mehmood, A. (2019). A new operation on soft sets: Extended difference of soft sets. Journal of New Theory, 27, 33-42.
Sezgin, A., & Atagün, A. O. (2011). On operations of soft sets. Computers and Mathematics with Applications, 61(5), 1457-1467.
Sezgin, A., & Atagün, A. O. (2023). A new soft set operation: Complementary soft binary piecewise plus (+) operation. Matrix Science Mathematic, 7(2), 125-142.
Sezgin, A., Atagün, A. O., Çağman, N., & Demir, H. (2022). On near-rings with soft union ideals and applications. New Mathematics and Natural Computation, 18(2), 495-511.
Sezgin, A., & Aybek, F. N. (2023). A new soft set operation: Complementary soft binary piecewise gamma operation. Matrix Science Mathematic, 7(1), 27-45.
Sezgin, A., Aybek, F. N., & Atagün, A. O. (2023a). A new soft set operation: Complementary soft binary piecewise intersection operation. Black Sea Journal of Engineering and Science, 6(4), 330-346.
Sezgin, A., Aybek, F. N., & Güngör, N. B. (2023b). A new soft set operation: Complementary soft binary piecewise union operation. Acta Informatica Malaysia, 7(1), 38-53.
Sezgin, A., & Çağman, N. (2024). A new soft set operation: Complementary soft binary piecewise difference operation. Osmaniye Korkut Ata University Journal of the Institute of Science and Technology, 7(1), 58-94.
Sezgin, A., Çağman, N., & Atagün, A. O. (2017). A completely new view to soft intersection rings via soft uni-int product. Applied Soft Computing, 54, 366-392.
Sezgin, A., Çağman, N., Atagün, A. O., & Aybek, F. N. (2023c). Complemental binary operations of sets and their application to group theory. Matrix Science Mathematic, 7(2), 114-121.
Sezgin, A., & Çalışıcı, H. (2024). A comprehensive study on soft binary piecewise difference operation. Eskişehir Teknik Üniversitesi Bilim ve Teknoloji Dergisi B - Teorik Bilimler, 12(1), 32-54.
Sezgin, A., & Dagtoros, K. (2023). Complementary soft binary piecewise symmetric difference operation: A novel soft set operation. Scientific Journal of Mehmet Akif Ersoy University, 6(2), 31-45.
Sezgin, A., & Demirci, A. M. (2023). A new soft set operation: Complementary soft binary piecewise star operation. Ikonion Journal of Mathematics, 5(2), 24-52.
Sezgin, A., & Sarıalioğlu, M. (2024). A new soft set operation: Complementary soft binary piecewise theta operation. Journal of Kadirli Faculty of Applied Sciences, 4(2), 325-357.
Sezgin, A., & Yavuz, E. (2023a). A new soft set operation: Complementary soft binary piecewise lambda operation. Sinop University Journal of Natural Sciences, 8(2), 101-133.
Sezgin, A., & Yavuz, E. (2023b). A new soft set operation: Soft binary piecewise symmetric difference operation. Necmettin Erbakan University Journal of Science and Engineering, 5(2), 189-208.
Singh, D., & Onyeozili, I. A. (2012). Some results on distributive and absorption properties on soft operations. IOSR Journal of Mathematics, 4(2), 18-30.
Stojanovic, N. S. (2021). A new operation on soft sets: Extended symmetric difference of soft sets. Military Technical Courier, 69(4), 779-791.
Tunçay, M., & Sezgin, A. (2016). Soft union ring and its applications to ring theory. International Journal of Computer Applications, 151(9), 7-13.
Vandiver, H. S. (1934). Note on a simple type of algebra in which the cancellation law of addition does not hold. Bulletin of the American Mathematical Society, 40(12), 914-920.
Yavuz, E. (2024). Soft binary piecewise operations and their properties (Master’s thesis). Amasya University, Graduate School of Natural and Applied Sciences, Amasya, Türkiye.
Zhu, P., & Wen, Q. (2013). Operations on soft sets revisited. Journal of Applied Mathematics, 2013, 1-7.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Suan Sunandha Rajabhat University

This work is licensed under a Creative Commons Attribution 4.0 International License.











